Los distintos tamaños del infinito

Desde que la humanidad ha mirado las estrellas, el concepto de infinito ha penetrado con fuerza en nuestras mentes. Lo que está más allá de nuestra imaginación, aquello que es inalcanzable e inabarcable… Todo ello, y mucho más, es en realidad el infinito.

Pero el infinito en matemáticas da para mucho. El matemático alemán Georg Cantor ha sido quien con más intensidad ha estudiado este concepto y la persona que, tal y como cuento en mi libro Historia del Infinito, ha logrado domesticar a la bestia.

Cantor tenía, entre otros, argumentos que le permitieron asegurar que hay infinitos de distintos tamaños. ¿Cómo es posible?

El infinito de lo numerable

Para comparar tamaños de conjuntos, la técnica probablemente más sencilla es emparejar objetos de uno y otro. Si cada elemento de un conjunto lo emparejamos con un elemento del otro (y no sobra ninguno), podremos asegurar que ambos conjuntos tienen la misma cantidad de elementos, es decir, tienen el mismo tamaño. En matemáticas decimos que hemos establecido una biyección.

Esta técnica del emparejamiento funciona muy bien con conjuntos finitos. Contar cosas no es más que establecer una niyección entre los primeros números naturales y eso que queremos contar.

Pero las biyecciones también son una buena forma de comparar tamaños de conjuntos infinitos. Y si de infinito hablamos, el conjunto que primero se nos viene a la cabeza es el de todos los números naturales. Cualquier conjunto que se pueda poner en biyección con los naturales se dice que es numerable.

Pero nuestra intuición nos puede jugar malas pasadas. Veamos algunos de los ejemplos que el propio Cantor se fue encontrando.

Los números racionales son las fracciones formadas por números enteros (evitando el cero en el denominador). De esta forma, todos los números naturales son, en particular, racionales. Pero… ¿cuántos racionales hay?

Uno de los primeros resultados sobre el infinito que Cantor demostró, siendo aún estudiante y como simple divertimento, fue que, en realidad, hay tantos números naturales como números racionales. Y esto a pesar de que los unos son una parte de los otros.

Comprobar esto es equivalente a dar una enumeración de los racionales, es decir, establecer cuál es el primero, el segundo, etc… Para ello, lo primero es darse cuenta de que basta con enumerar los racionales positivos (claro, porque siempre podemos hacer: cero, positivo, negativo, positivo, negativo,…).

El argumento que se atribuye a Cantor es simple, pero efectivo. Ponemos en una fila todos los racionales con denominador 1, en la segunda fila los de denominador 2, en la tercera los de denominador 3 y así sucesivamente. De esta forma tendremos todos los racionales en una suerte de tabla sin fin, aunque habrá muchos que aparecen repetidos (no importa, luego se quitarán). Ahora, una simple línea en forma de zigzag recorriendo todos los números de la tabla hará las veces de enumeración.

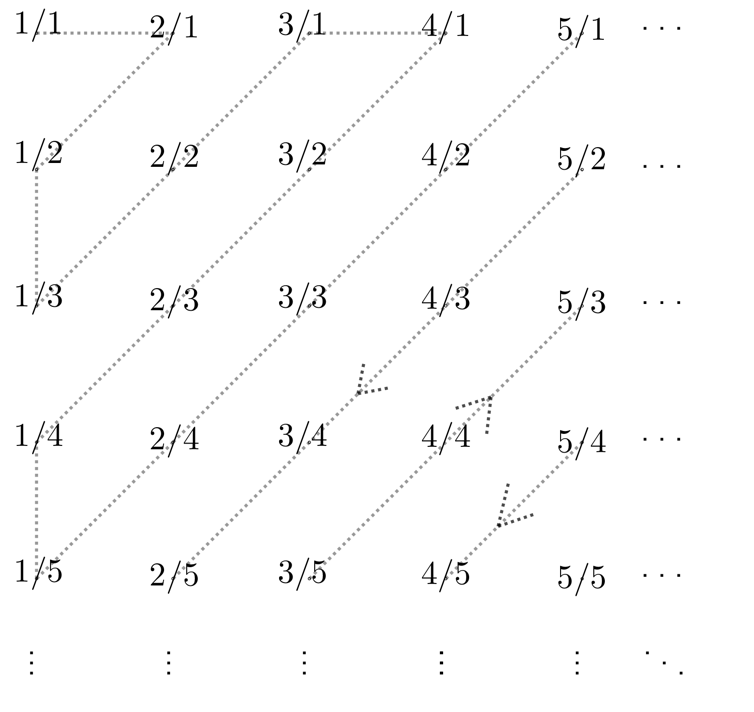
Hay, pues, tantos números naturales como racionales.

El infinito del continuo

Pero si dibujamos en la recta todos los números racionales, resulta que prácticamente la llenan. En realidad, tan cerca como queramos de cualquier número (real) hay un racional. Esta propiedad se conoce como densidad de los racionales en los reales.

Así que Cantor, buen conocedor de este hecho, se preguntó si sería posible enumerar la totalidad de los números reales. Dado que parece que lo que le falta a los racionales para llenar la recta es prácticamente nada, resulta una pregunta de lo más natural (nunca mejor dicho).

Vamos a quedarnos no con todos los números reales, sino los que están entre 0 y 1. Estos números tienen la peculiaridad de que todos pueden escribirse en forma decimal comenzando con un 0 (recordad que 1=0,999…).

Cantor propone el siguiente argumento. Supongamos que podemos enumerar a todos los números reales entre 0 y 1 y que los ponemos en una lista. Por ejemplo:

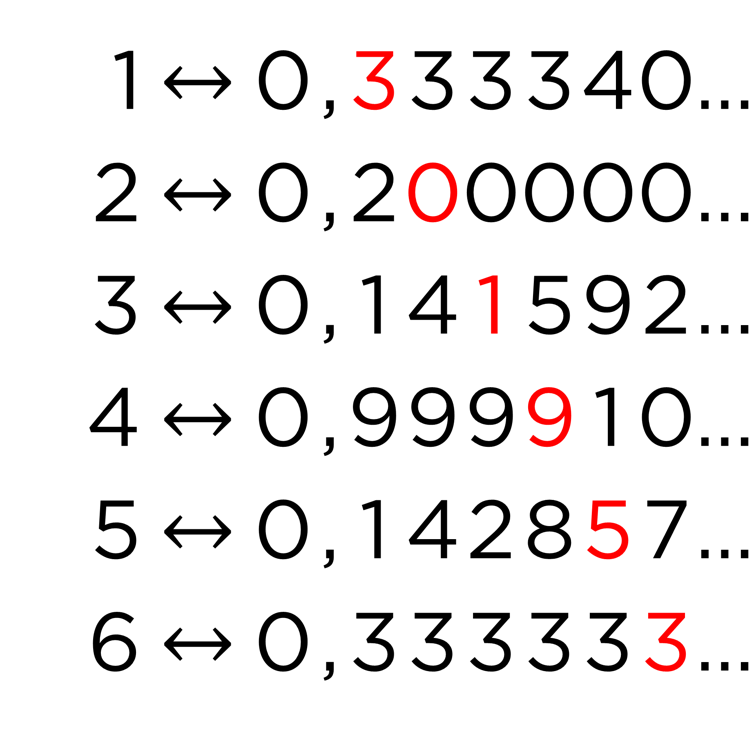
Pues bien, basándose en esa lista, Cantor construye un nuevo número.

Fijémonos en el primer decimal del primer número (el que está en rojo), el 3 en este caso. Para su número, Cantor toma como primer decimal cualquier dígito que no sea el 3, por ejemplo, el 4.

Repetimos el argumento con el segundo decimal del segundo número, el 0; Cantor toma, por ejemplo el 1. Como el tercer decimal del tercer número es el 1, tomamos para nuestro número el 2, por ejemplo. Y así sucesivamente seguimos con todos los números de la lista. De esta forma, construimos el número 0,412064…

Pero, ¿qué tiene de especial ese número? Pues que no está en la lista. En efecto, como el primer decimal es diferente del primer número de la lista, no puede ser el primero; como el segundo decimal es diferente del segundo de la lista, tampoco puede ser el segundo; ni el tercero, pues difiere del tercer decimal; ni el cuarto, ni el quinto…

En definitiva, lo que Cantor demuestra es que sea cual sea la forma de enumerar los números entre el 0 y el 1, siempre se nos va a escapar al menos uno. Dicho de otro modo, resulta imposible establecer una biyección entre los reales (entre 0 y 1) y los naturales.

Y dado que hay más reales que naturales, Cantor concluye que el infinito del continuo, el de los números reales, es más grande que el infinito de los números naturales.

Tenemos infinitos de diferentes tamaños.

Toda una sucesión de infinitos cada cual más grande que el anterior

Este argumento de Cantor no fue el primero que publicó. El original era mucho más complicado y técnico y le trajo no pocos contratiempos (esta historia la podéis leer también en Historia del Infinito).

Para resarcirse, el argumento diagonal (que así se conoce al que hemos visto), ofrece en realidad una forma de generar un infinito más grande que cualquiera dado. Es lo que se conoce como Teorema de Cantor.

Cantor no solo establece la existencia de un infinito más grande que otro. Demuestra que hay toda una sucesión de infinitos cada cual más grande que el anterior.

José Antonio Prado Bassas, Profesor Titular de Universidad en el Dpto. Análisis Matemático, Universidad de Sevilla

Este artículo fue publicado originalmente en The Conversation. Lea el original.